• 介绍
  • 查询操作
  • 插入操作
  • 删除操作
  • 实现思路
  • 总结

介绍

对于链表，无法像数组一样可以进行二分查找，但是可以在链表的基础上做一个小升级。相当于一个链表拥有自己的索引。

查询操作

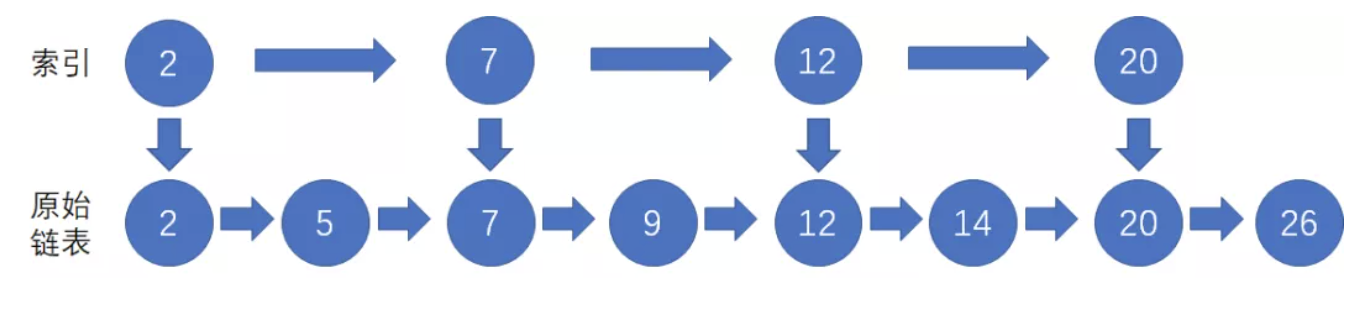
如图所示，在原始链表的基础上，我们增加一个索引链表。原始链表的每2个节点，有一个节点也在索引链表当中。 当我们想要定位到节点20，我们不需要在原始链表中一个个节点访问，而是先访问索引链表：

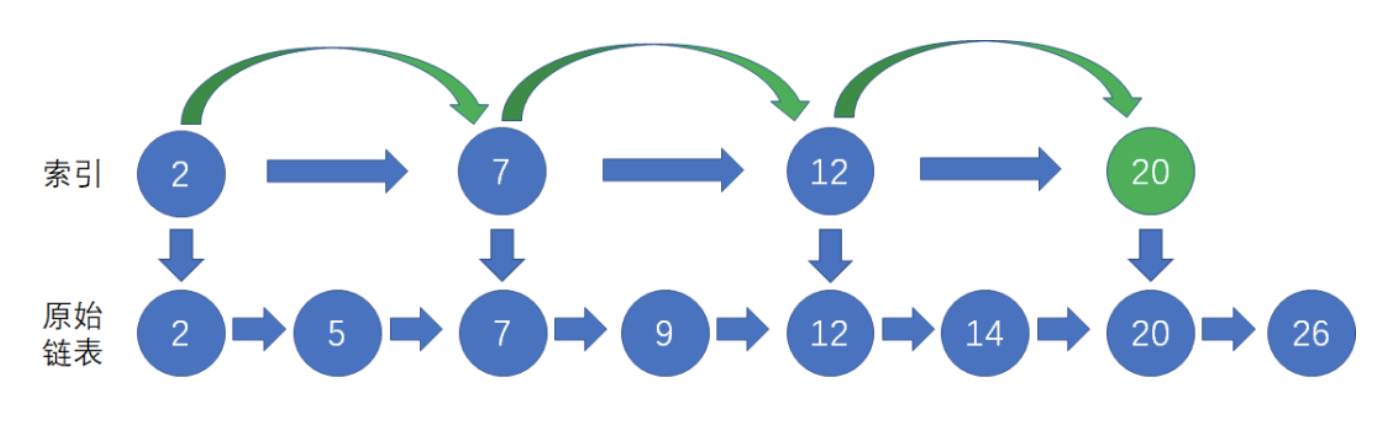
在索引链表找到节点20后，我们顺着索引链的节点向下，找到原始链表的节点20

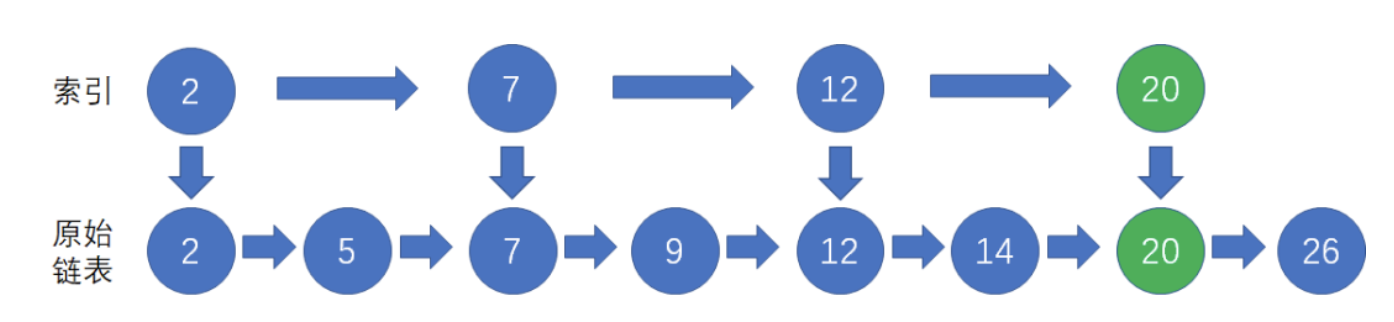
这个过程，就像是先查阅了目录，再找到对应的页码。

由于索引链表的节点个数是原始链表的一半，查找节点所需要的访问次数也相应减少了一半。

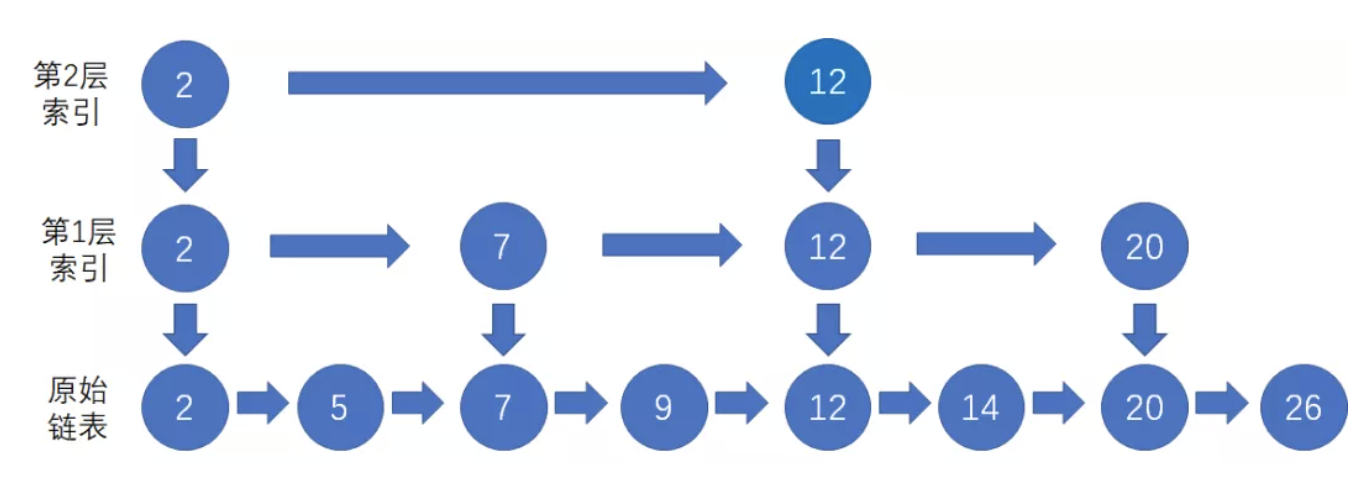
而且我们可以基于原始链表的第一层索引，抽出第二层更为稀疏的索引，节点数量是第一层的一半

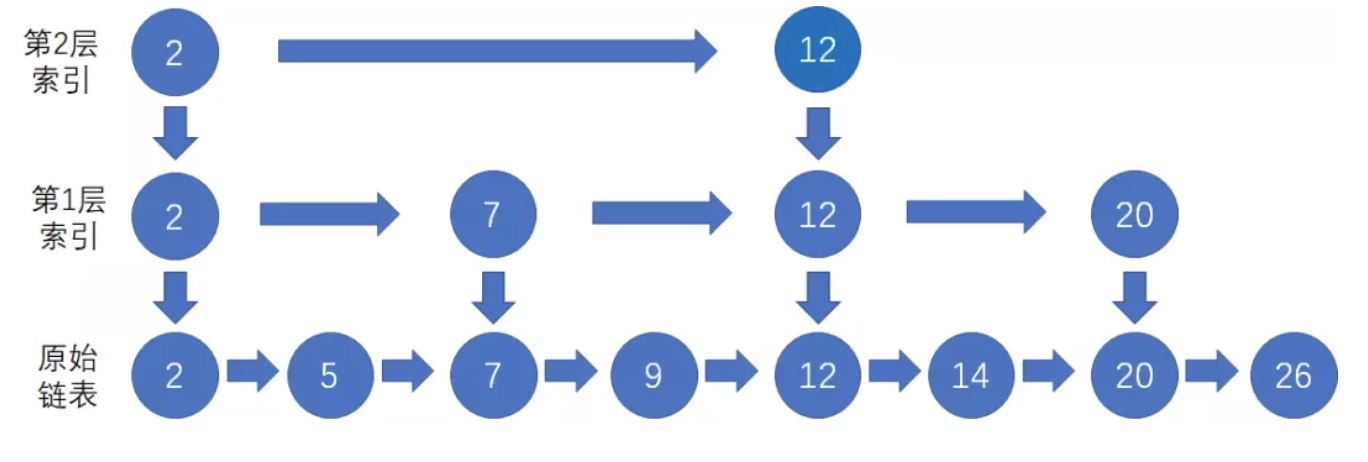
这样的多层索引可以进一步提高查询效率，如果仍要查询节点20。

我们先从最上层的索引开始查找，找到该层中仅小雨节点20的前置索引12；

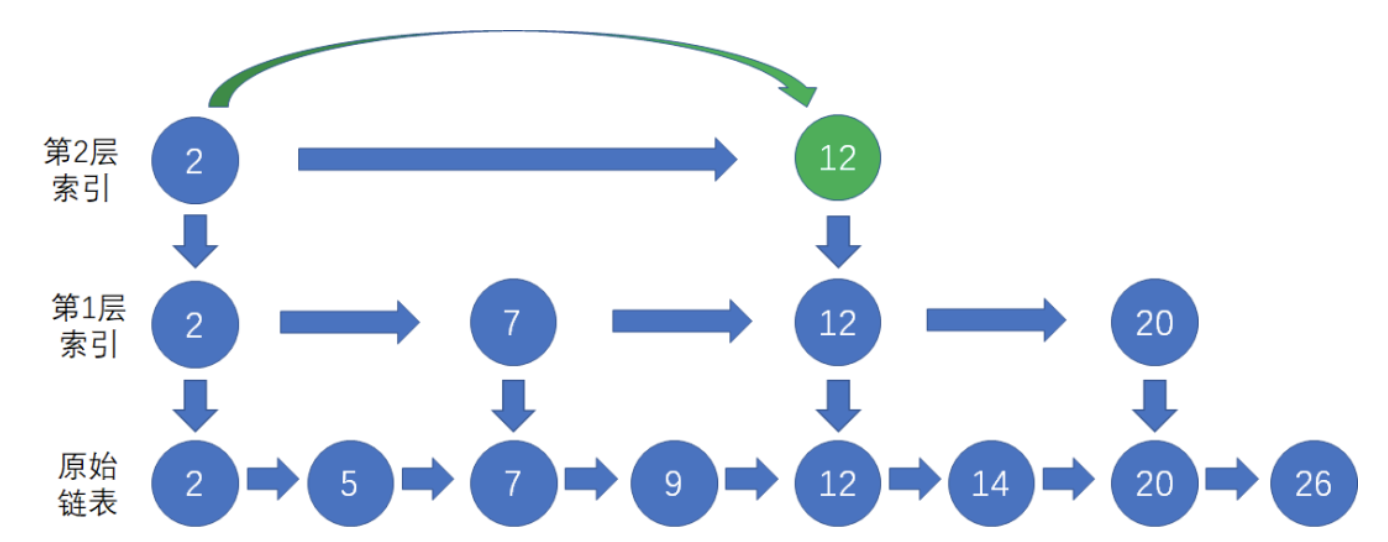
我们顺着节点12访问下一层索引，在该层中找到节点20；

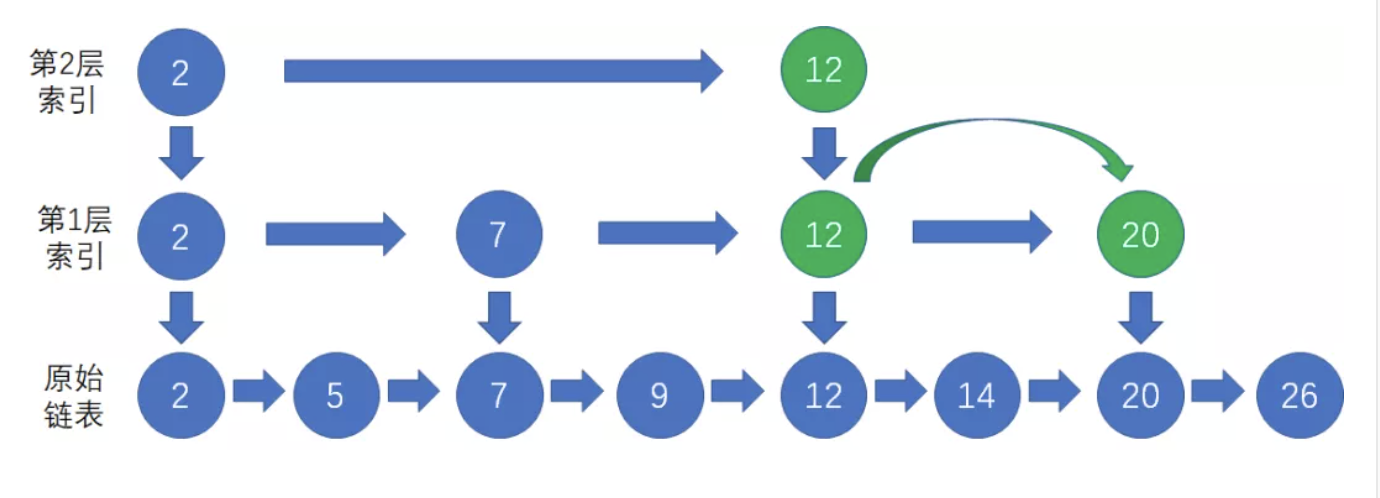
最后，顺着第1层的索引节点20向下，找到原始链表的节点20；

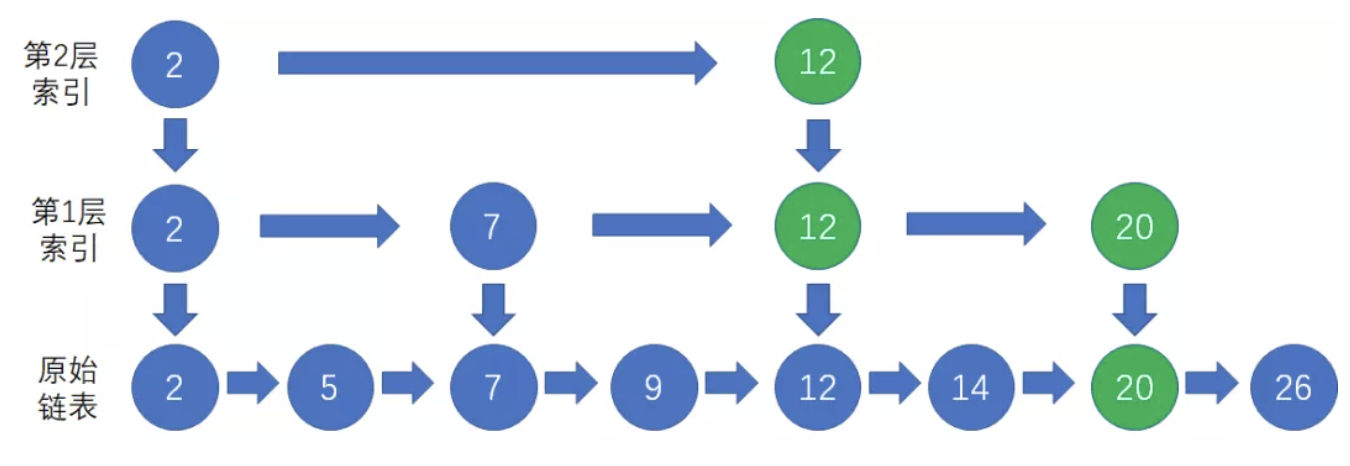
在这个例子中，由于原始链表的结点数量较少，仅仅需要2层索引。如果链表的结点数量非常多，我们就可以抽出更多的索引层级，每一层索引的结点数量都是低层索引的一半。

假设原始链表有n个节点，那么索引的层级就是log(n)-1，在每一层的访问次数是常量，因此查找节点的平均复杂度是O(logn)。这比起常规的查找方式，也就是线性依次访问链表节点的方式效率要高。

但是相应的，这种基于链表的优化增加了额外的空间开销。这是典型的空间换时间。

插入操作

假设我们要插入的节点是10，首先按照跳表的查找节点的方法，找到待插入节点的前置节点(小于待插入节点)

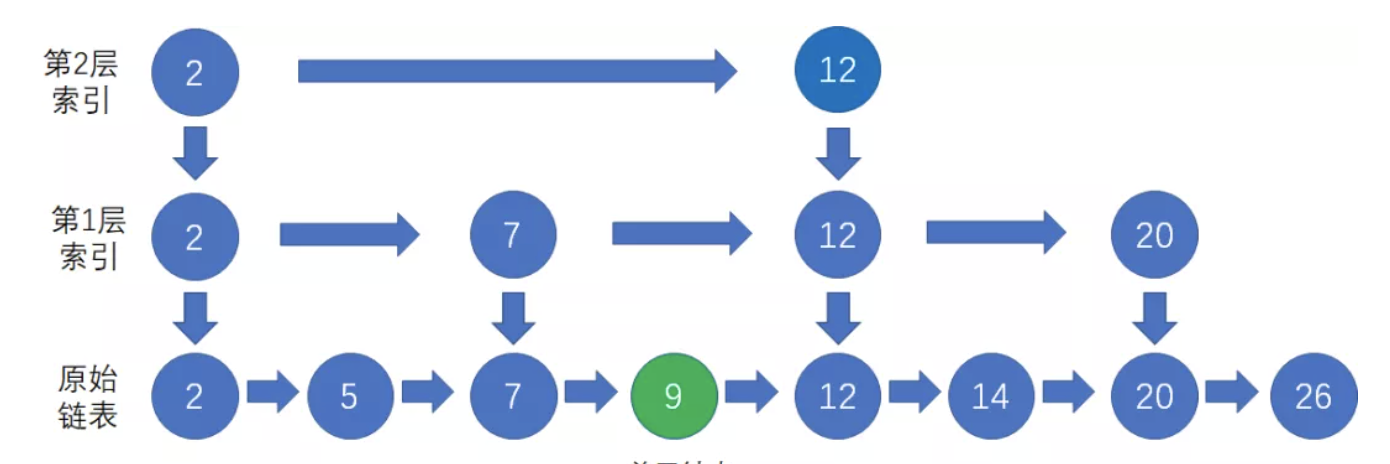
按照链表的一般插入方式，把节点10插入到节点9的下一个位置。

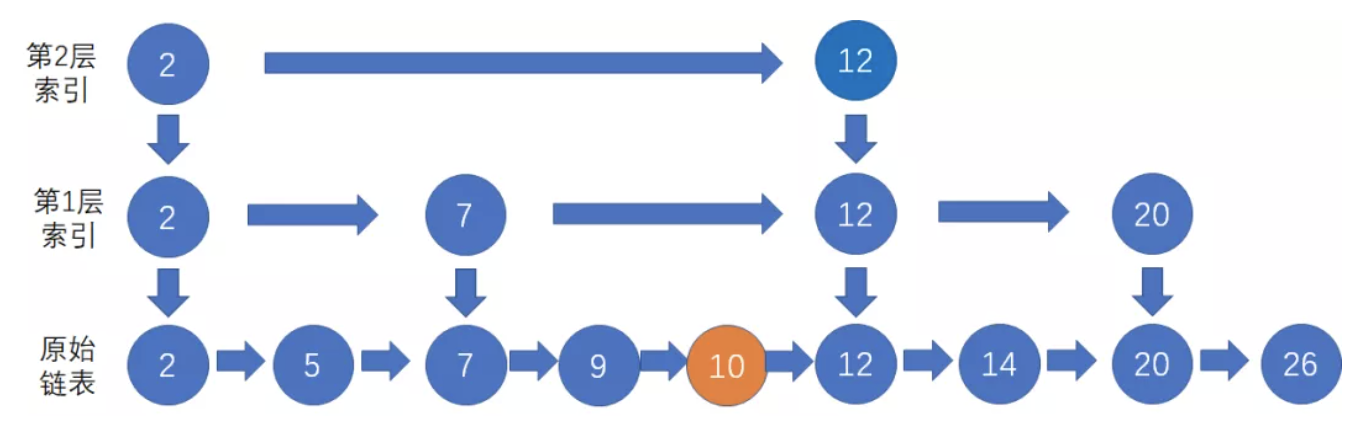
随着原始链表的节点越来越多，索引会变得渐渐不够用了，因此索引节点也需要相应作出调整。

我们让新插入的节点随机晋升，也就是成为索引节点。新节点晋升的成功率是50%

假设第一次随机的结果是晋升成功，我们把节点10作为索引节点，插入到第1层索引的对应位置，并且向下指向原始链表的节点10

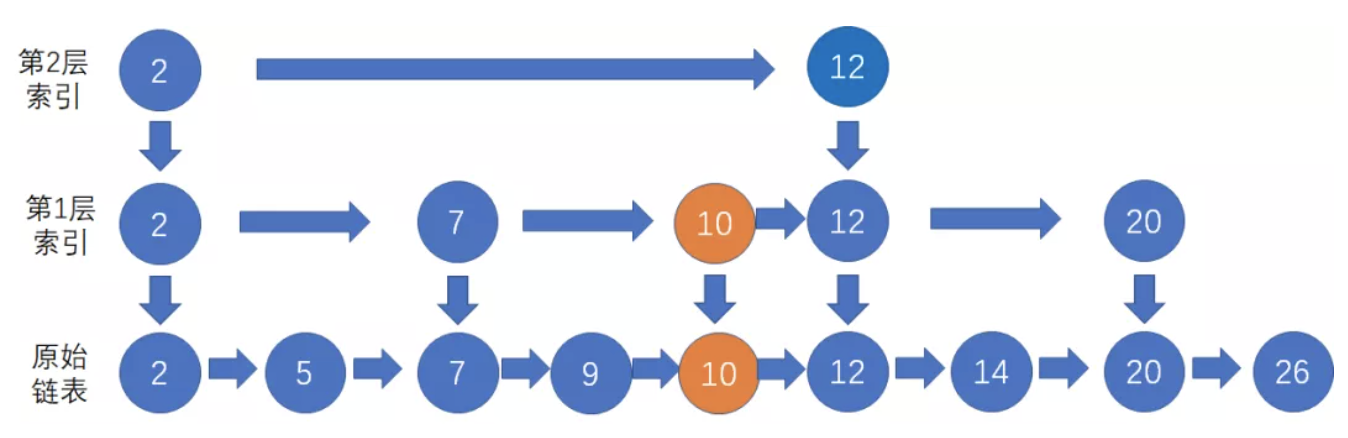
新节点成功晋升之后，仍有机会继续向上一层索引晋升。如果随机的结果是晋升失败，那么插入结束。

如果节点10已经晋升到第2层索引，下一次随机的结果依旧成功晋升

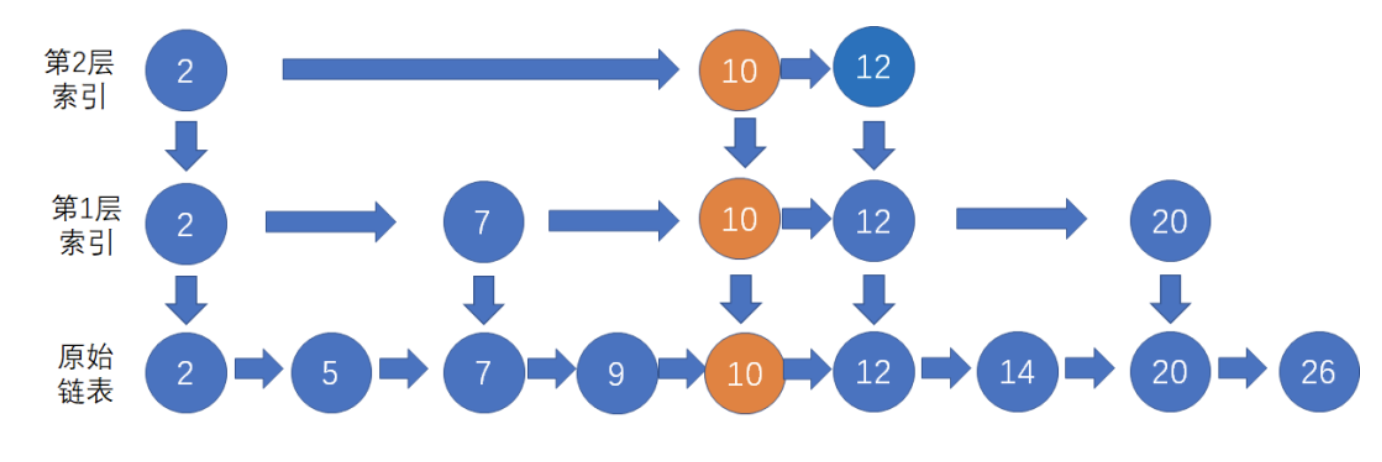
这个时候直接让索引增加一层

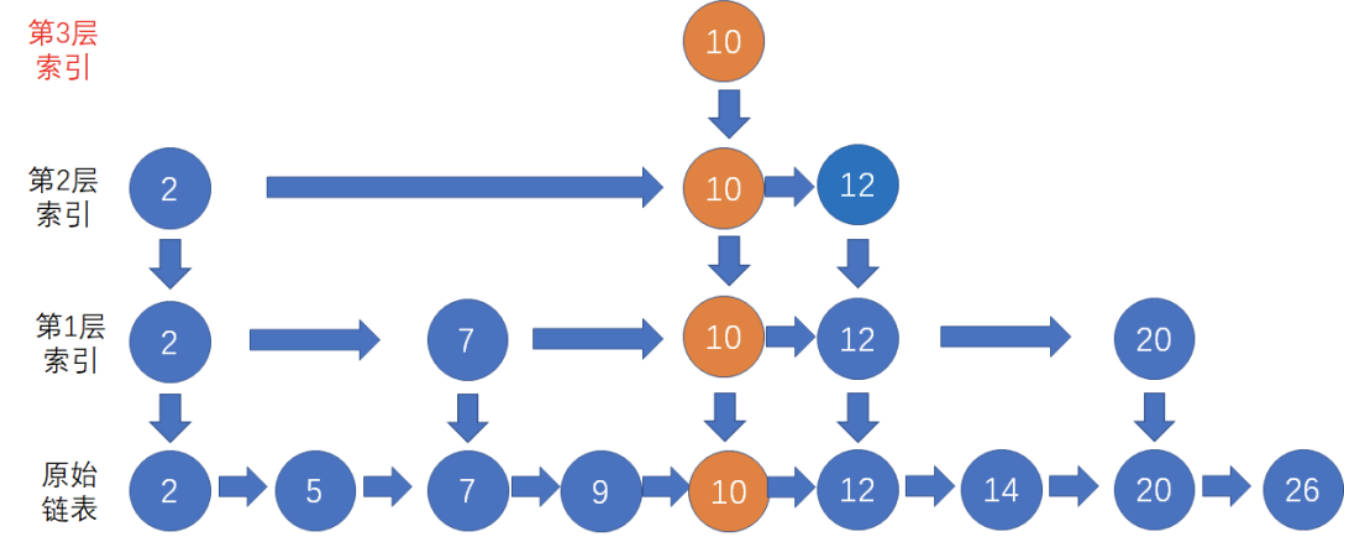
删除操作

假设要从跳表删除节点10 ，首先要按照跳表查找节点的方法，找到待删除的节点

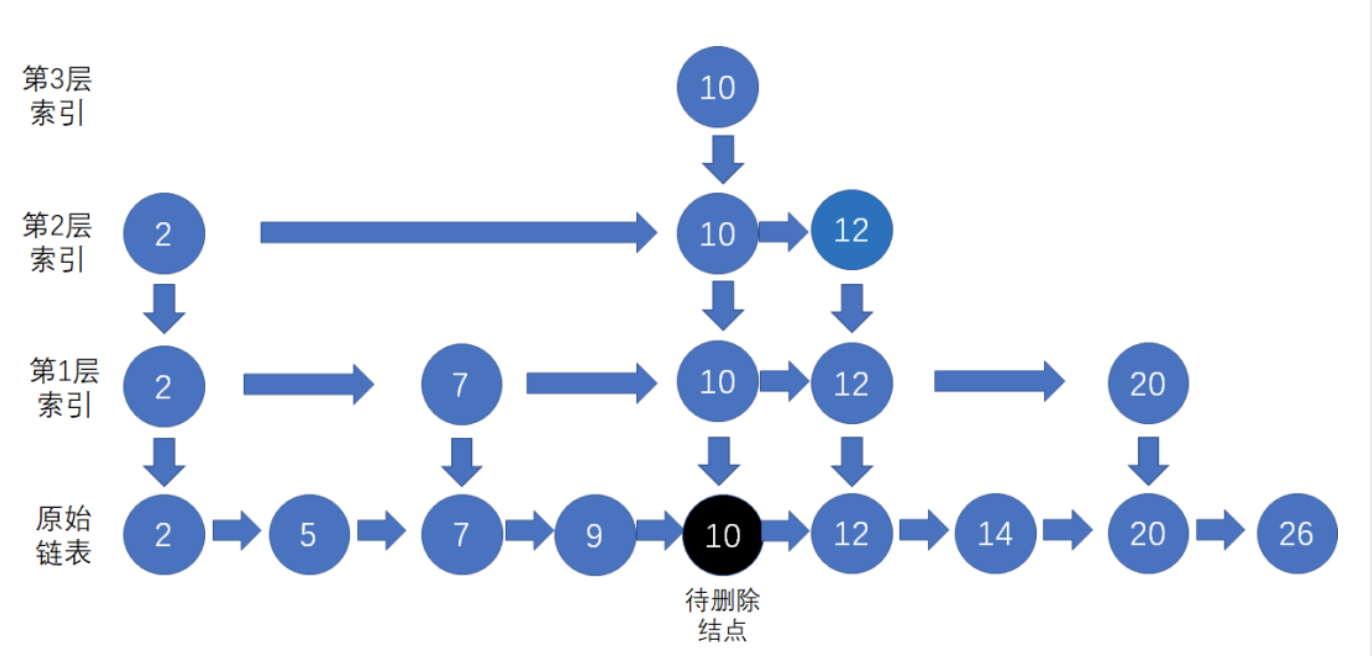
按照一般链表的方式，把节点10从原始链表当中删除

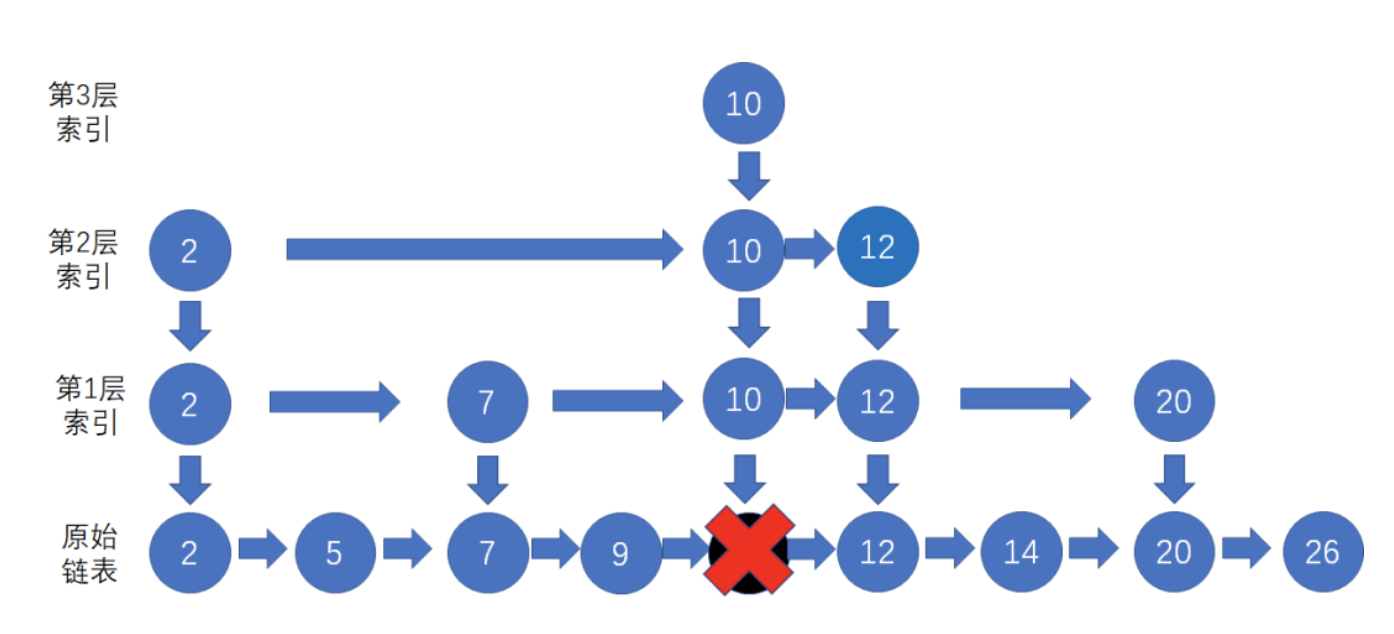
之后我们需要一层层往上，把索引中对应的节点也删除

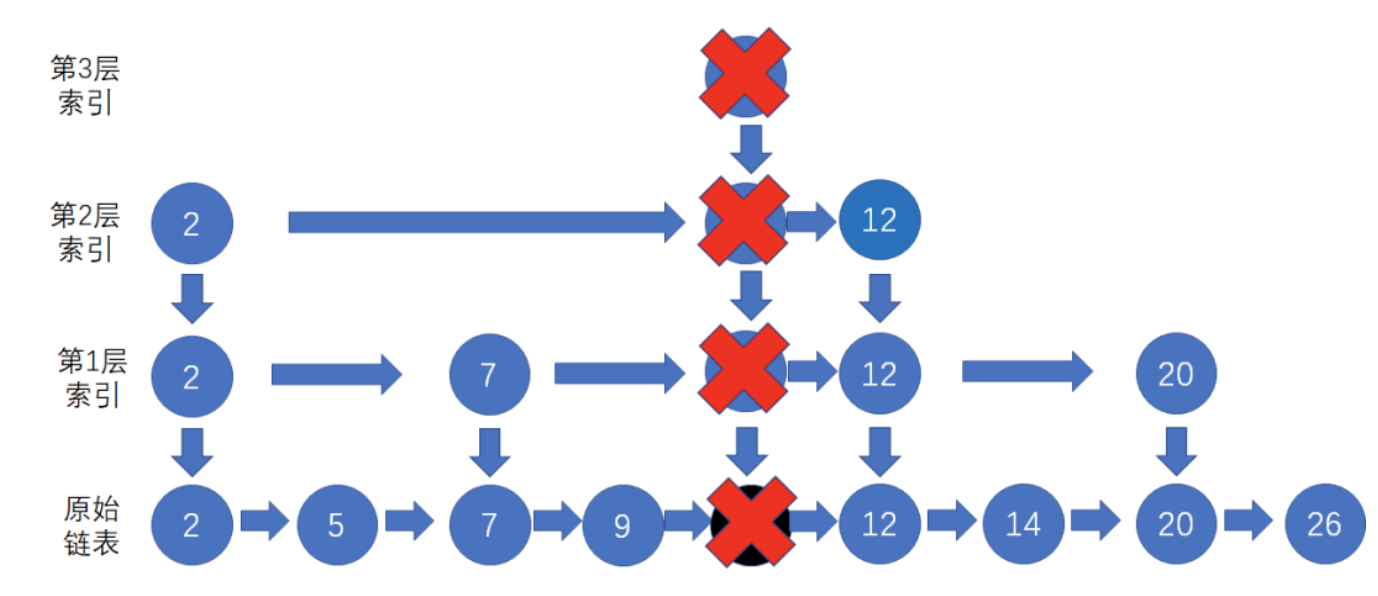
如果某一层的索引节点被删除完了，直接把失去节点的那一层给删除

根据刚才的例子，第3层索引节点没有了，因此我们把整个第3层删除

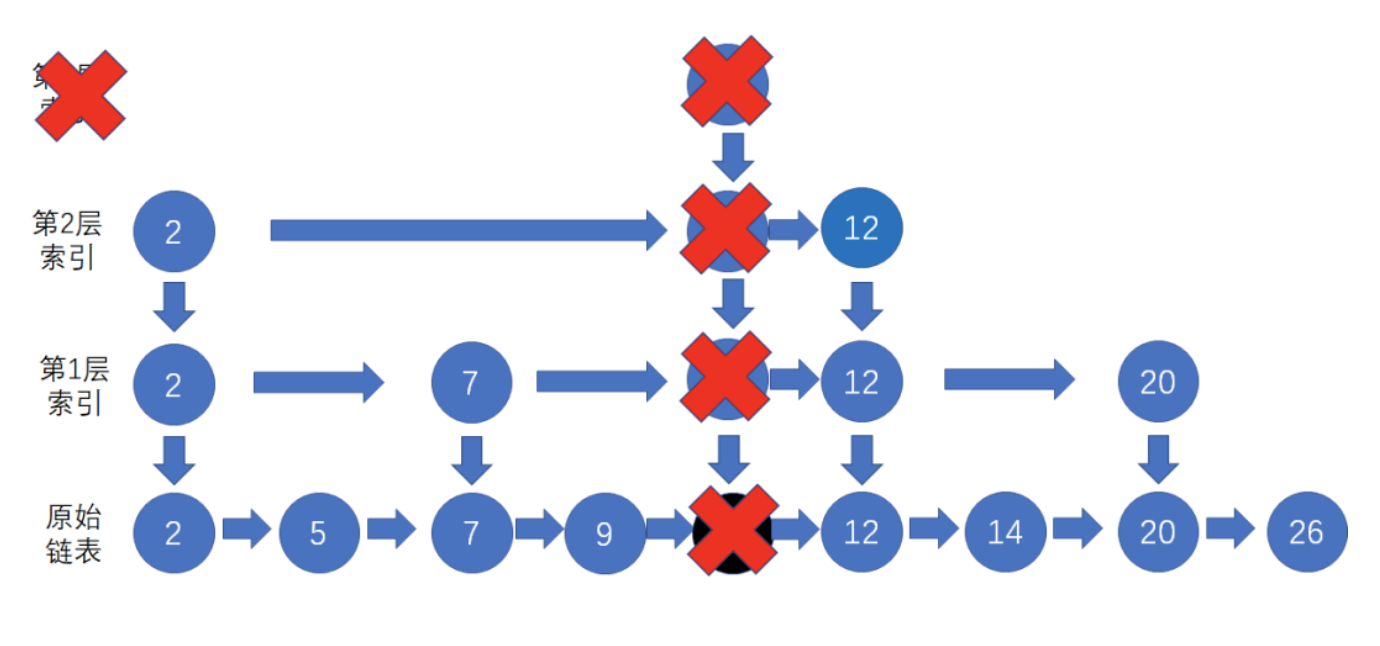
最终删除结果如下

实现思路

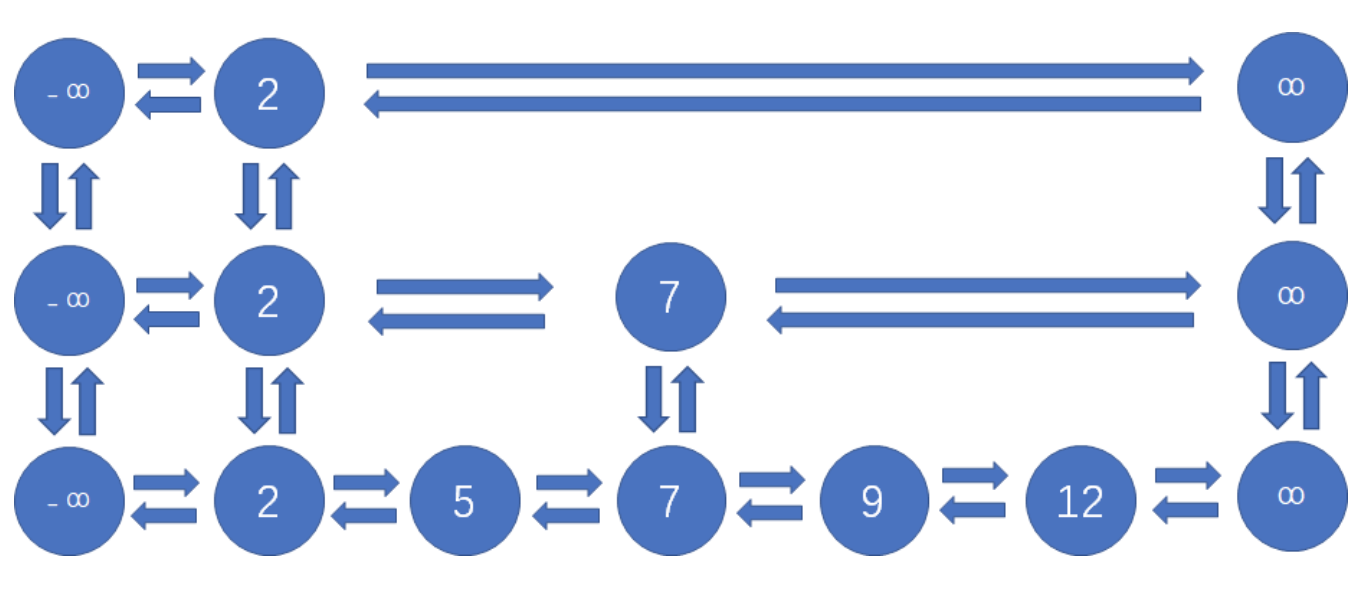
1. 程序中跳表使用的双向链表，无论前后节点还是上下节点，都有各个两个指针指向彼此；
2. 程序中跳表的每一层首位各有一个空节点，左侧空节点负无限大，左侧空节点正无限大；

总结

跳表是基于链表的升级，使一个有序链表获得了高效增删改查，并始终维持有序的能力，功能与性能跟红黑树相似。